热电效应 - Thermoelectric effect

热电效应（英语：Thermoelectric effect）是指由温度差直接产生的电压差，或者由电压差直接产生的温度差。这个效应可以用来产生电能、测量温度，冷却或加热物体。因为加热或制冷的方向取决于施加电压的方向，热点装置让温度控制变得非常容易。

一般情况下，热电效应总共包含了三个分别经过定义的效应：塞贝克效应（Seebeck effect，由 Thomas Johann Seebeck 发现）、帕尔贴效应（Peltier effect，由 Jean-Charles Peltier 发现）、汤姆孙效应（Thomson effect，由 William Thomson 发现）。在很多教科书上，热电效应也被称为 帕尔贴-塞贝克效应（Peltier-Seebeck effect）。此效应由法国实验物理学家 Jean-Charles Peltier 与爱沙尼亚裔德国物理学家 Thomas Johann Seebeck 分别独立发现。同时还有一个术语叫作 焦耳热 ，即当一个电压通过某一阻抗物质上会产生热量，其值与电流 I 的平方、导体的电阻 R 和通电时间 t 成比例关系。 帕尔贴-塞贝克效应 与 汤姆孙效应 是热力学可逆的，但是 焦耳热 并不是可逆的。

塞贝克效应

德国物理学家托马斯·约翰·塞贝克于1821年发现，将二种不同金属各自的二端分别连接构成的回路，如果两种金属的两个结点处温度不同，就会在这样的线路内发生电流。这种现象称为赛贝克效应(Seebeck Effect)。

Seebeck effect

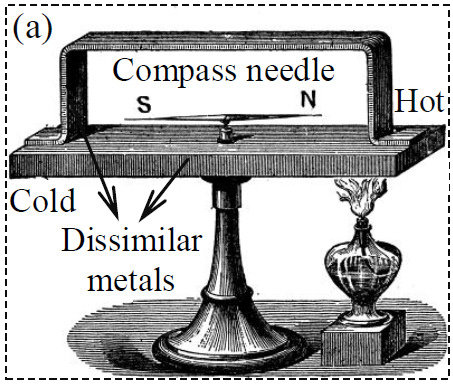
塞贝克发现，当两种不同金属组成闭合回路且两结点处温度不同时，指南针的指针会发生偏转。于是他认为温差使金属产生了磁场。但是当时塞贝克并没有发现金属回路中的电流，所以他把这个现象叫做“热磁效应”。后来，丹麦物理学家汉斯·奥斯特重新研究了这个现象并称之为“热电效应”。

不同的金属导体（或半导体）具有不同的自由电子密度，当两种不同的金属导体相互接触时，在接触面上的电子就会扩散以消除电子密度的差异，在两块金属的另两个端点形成稳定的电压，电子的扩散速率与接触区的温度成正比。由此产生的电压通常每开尔文温差只有几微伏。 而不同温度的相同金属（或半导体）也具有不同的自由电子密度，所以只要维持金属两端的温差，也能使电子持续扩散，在金属的两个端点形成稳定的电压。

不同的金属与半导体具有不同的塞贝克系数（所产生赛贝克效应大小不同），半导体与金属的主因略有不同。半导体在不同的温度下具有不同的载流子密度，当单一半导体两端具有温度差时，载子会扩散以消除密度的差异，因而造成电动势。两端的温度相差越大，则产生的赛贝克电位差越大。而金属的自由电子密度与费米能级几乎不会随温度改变，因此金属的赛贝克效应远小于半导体。金属的赛贝克效应由电子的平均自由程来决定。若平均自由程随温度上升，则热端的自由电子有较高的机会向冷端移动，此时的塞贝克系数为负值。反过来说，若电子的平均自由程随温度上升而下降，则冷端的自由电子有较高的机会流向热端，塞贝克系数为正值。

在以下电路中，若电压计两端的温度同为 $T_{r}$ ：

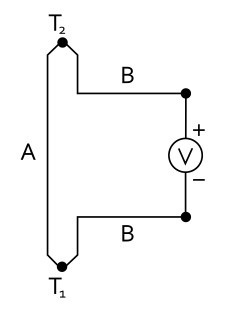
由塞贝克效应产生的电压可以表示成：

$$V = \int_{T_{1}}^{T_{r}}S_{B}(T)dT + \int_{T_{2}}^{T_{1}}S_{A}(T)dT + \int_{T_{r}}^{T_{2}}S_{B}(T)dT = \int_{T_{1}}^{T_{2}}\left(S_{B}(T) - S_{A}(T)\right)dT$$

其中， $S_A \text{、} S_B$ 是金属 A 和 B 的塞贝克系数， $T_1 \text{、} T_2$ 是两块金属结合处的温度。塞贝克系数取决于温度和材料的分子结构。如果塞贝克系数在实验的温度范围内接近常数，以上方程可以近似成：

$$V = \left(S_B - S_A\right) \cdot \left(T_2 - T_1\right)$$

• 将两种不同的金属连接，并在两接点给予温度差，两种金属会分别产生各自的温差电动势。
• 选用适当的二种不同金属制成热电偶，利用赛贝克效应可以直接测量温差，或者将金属的一端设定到已知温度来测另一端的温度。
• 当几个温差电偶连接在一起时叫做热电堆，用来制造更大的电压。
• 塞贝克效应还可以用来鉴定合金的成分：将未知金属和已知金属连接，并保持温度不变，根据测得的电压可以算出未知金属的塞贝克系数，从而判断它的材料。
• 若使用相同的金属形成回路，则会因为温差造成的电动势互相抵销而无法观察到赛贝克效应。

帕尔贴效应

传统上有时称 帕尔贴效应 是 塞贝克效应 ，但此说法并不严谨。与 塞贝克效应 不同， 帕尔贴效应 可以产生在两种不同金属的交界面，或者一种多相材料的不同相界间，也可以产生在非匀质导体的不同浓度梯度范围内。

Peltier effect

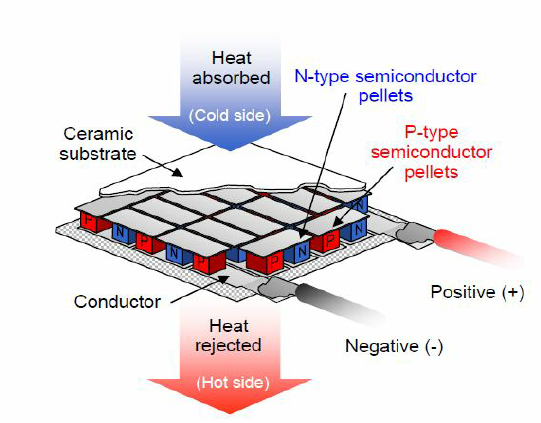
当对上述三种材料嵌入回路中并施加电流时，金属 1 会对金属 2 或相 1 对相 2，或浓度点 C1 与 C2 间产生放热或吸热反应。帕尔帖效应即为塞贝克效应的反效应，即当在两种金属回路中加入电源产生电势后，不同的金属接触点会有一个温差。

半导体制冷片（帕尔贴）

汤姆孙效应

当电流在温度不均匀的导体中流过时，导体除产生不可逆的焦耳热之外，还要吸收或放出一定的热量（称为汤姆孙热）。汤姆孙效应（英语：Thomson effect）是英国物理学家 William Thomson 于 1854 年发现的：将一根导线通恒定电流，由于导线有电阻而发热。再将这根带电的导线的某小局部加热；使它产生温度梯度。这根导线就在原有发热的基础上，出现吸热或放热的现象。或者反过来，当一根金属棒的两端温度不同时，金属棒两端会形成电势差。

一个金属(或半导体)材料的帕尔帖系数并不是一个定值，也会随着温度而改变。在一个具有温度梯度的导体中，每个位置都可以视为是具有不同帕尔帖系数的材料。当电流通过时，不同的位置会各自产生帕尔帖效应，造成局部的吸热或放热。由于金属的热导率较高，这些局部的吸收或放出的热能会分散至整个导体，因而造成导体整体的吸热或放热。吸热或放热要由恒定电流的方向和导线热梯度的方向而决定。这种现象称为汤姆孙效应，汤姆孙效应并不会在均匀温度的通电流导体中出现。

完整热电方程

真正的热电装置通常会涉及到多种上述效应的操作。我们可以用种一致而严谨的方式将塞贝克效应、帕尔帖效应和汤姆逊效应结合起来;同时包含焦耳加热和普通热传导的影响。 如上所述，塞贝克效应会产生电动势，进而得到电流方程：

$$\mathbf{J} = \sigma\left(-{\nabla}V - S{\nabla}T\right)$$

为了描述帕尔帖效应和汤姆孙效应，我们必须考虑能量流。如果温度和电荷随时间变化，则能量累积量 $\dot{e}$ 的完整热电方程如下：

$$\dot{e} = \nabla \cdot (\kappa \nabla T) - \nabla \cdot (V + \mathrm{II})\mathbf{J} + \dot{q}_{ext}$$

$\kappa$ 是热导率，第一项是傅里叶热传导定律，第二项表示电流携带的能量。第三项 $\dot{q}_{ext}$ 是从外部热源输入的热量（如果适用的话）。

材料若达到稳态，那么电荷和温度就呈现稳定的分布，此时 $\dot{e} = 0$ ， $\nabla \cdot \mathbf{J} = 0$ 。利用这些事实和第二汤姆孙关系（见下文），可以将热方程简化如下：

$$- \dot{q}_{ext} = \nabla \cdot (\kappa \nabla T) + \mathbf{J} \cdot (\sigma^{-1}\mathbf{J}) - TJ \cdot \nabla S$$

中间项是焦耳热，最后一项包括帕尔帖效应（在交界处的 $\nabla S$ ）和汤姆孙效应（在热梯度中的 $\nabla S$ ）。结合塞贝克方程 $\mathbf{J}$ ，该方法可用于求解复杂系统的稳态电压分布和温度分布。

如果物质不是处于稳定状态，那么完整的描述则需要纳入动态效应，比如与电容、电感和热容有关的动态效应。