热量传递 - Heat transfer

热传分析

热传递以其所有模式（即传导，对流和辐射）发生，一般运输方程的微分形式如下：

$$\frac{\partial (\rho \phi)}{\partial t} + div(\rho u \phi) = div(k \text{ } grad\phi) + S_{\phi}$$

可以通过有限差分法（FDM），有限体积法（FVM）和有限元素法（FEM）获得上述方程的数值解。为了进行传热分析，将上述等式中的标量函数 $\phi$ 替换为温度 $T$ ，将扩散系数 $\Gamma$ 替换为热导率 $k$ 和 源项 $S_{\phi }$ 由发热项 $e$ 或任何热辐射源代替 $Q_{i}$ 或两者兼而有之（取决于可用来源的性质），并且针对不同情况存在不同形式的方程式。为了简单和容易理解，仅讨论了一维情况。

可以通过两种方式对物体进行热传分析： 稳态热分析；瞬态热分析。

稳态热分析

在这种分析中，只关心物体达到热平衡状态时的热力条件，而不关心达到这种状态所用的时间。达到热平衡时，进入模型中每个点的热能与离开该点的热能相等。一般来说，稳态分析所需的唯一材料属性是热导率。
稳态热分析包括以下类型的微分方程。

• 情况1： 一般稳态导热方程。
  在这种情况下，微分方程变为： $div(\rho u T) = div(k \text{ } gradT) + S_{T}$ .

• 情况2： 稳态热传导方程（不产生热量）
  在这种情况下，微分方程变为： $div(\rho u T) = div(k \text{ } gradT)$ .

• 情况3： 稳态热传导方程（不产生热，不对流）
  在这种情况下，微分方程变为： $div(k \text{ } gradT) = 0$ .

瞬态热分析

在这种分析中，只关心模型的热力状态与时间的函数关系。 例如，热水瓶设计师知道里面的流体温度最终将与室温相等（稳态），但热水瓶设计师感兴趣的是找出流体的温度与时间的函数关系。 在指定瞬态热分析的材料属性时，需要指定热导率、密度和比热。 此外，还需要指定初始温度、求解时间和时间增量。
瞬态热分析包括以下类型的微分方程。

• 情况1： 瞬态热传导
  在这种情况下，微分方程变为： $\dfrac{\partial (\rho T)}{\partial t} + div(\rho u T) = div(k \text{ } gradT) + S_{T }$ .

• 情况2： 瞬态热传导（不产生热）
  在这种情况下，微分方程变为： $\dfrac{\partial (\rho T)}{\partial t} + div(\rho u T) = div(k \text{ } gradT)$ .

• 情况3： 瞬态热传导（不产生热也没有对流）
  在这种情况下，微分方程变为： $\dfrac{\partial (\rho T)}{\partial t} = div(k \text{ } gradT)$ .

热传方式

热传（heat transfer）有三种方式：

• 热传导（heat conduction）：一个分子向另一个分子传递振动能，使热能从高温向低温部分转移。各种材料的热传导性能不同，传导性能好的，如金属，还包括了自由电子的移动，所以传热速度快，可以做热交换器材料；传导性能不好的，如石棉，可以做热绝缘材料。
• 热对流（heat convection）：是指由于流体的宏观运动而引起的流体各部分之间发生相对位移，冷热流体相互掺混所引起的热量传递过程。不同的温度导致引起系统的密度差是造成对流的原因。对流传导因为牵扯到动力过程，所以比直接传导迅速。
• 热辐射（heat radiation）：是直接通过电磁波辐射向外发散热量，传导速度取决于热源的绝对温度，温度越高，辐射越强。

根据传热的方式和工艺要求，设计热交换器，几乎各种化学工业都有热交换过程，需要各种热交换器。

热传导

热传导，是指在物体内部或相互接触的物体表面之间，由于分子、原子及自由电子等微观粒子的热运动，而产生的热量传递现象，是热能从高温向低温部分转移的过程，是一个分子向另一个分子传递振动能的结果。各种材料的热传导性能不同，传导性能好的，如金属，还包括了自由电子的移动，所以传热速度快，可以做热交换器材料，而金属传导能力依次为银 ＞ 铜 ＞ 金 ＞ 铝；传导性能不好的，如石棉，可以做热绝缘材料。

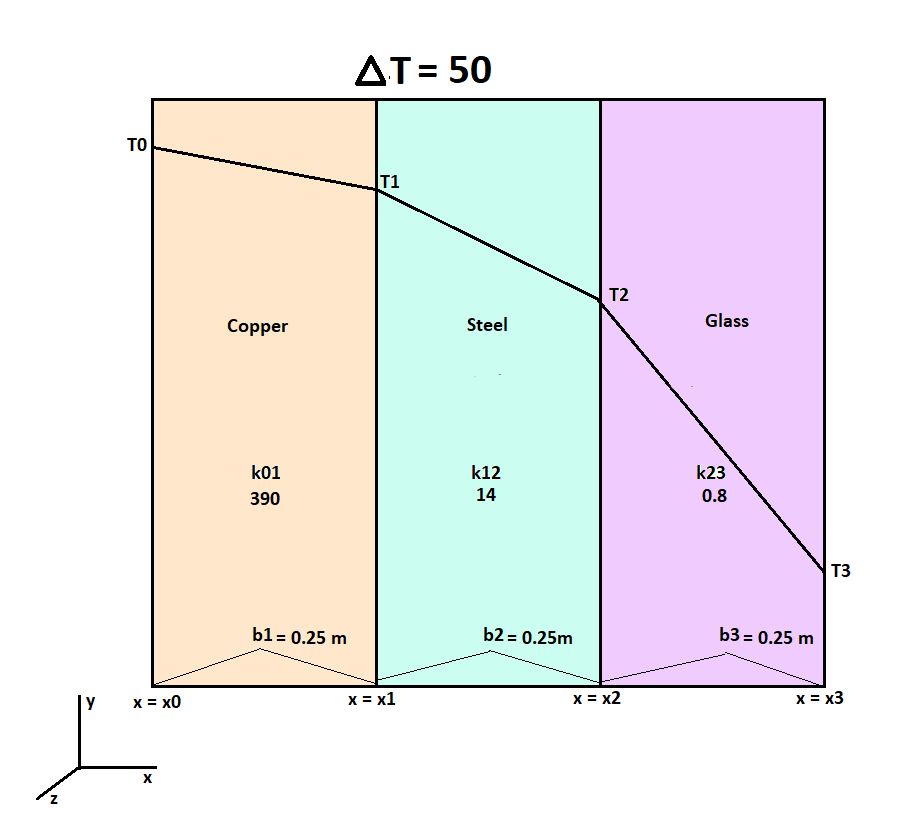
一维稳态导热

在工业和日常生活中，大平壁的导热是最简单、最常见的导热问题，例如通过炉墙以及房屋墙壁的导热等。当平壁两表面分别维持均匀恒定的温度时，可以近似地认为平壁内的温度只沿着垂直于壁面的方向发生变化，并且不随时间而变，热量也只沿着垂直于壁面的方向传递，如下图所示，这样的导热称为一维稳态导热。

傅里叶定律

热传导定律，也称为傅立叶定律，描述了热量在介质中的传导规律。其形式与电传导欧姆定律相似。 傅立叶定律可以以两种形式表述：微分形式关注于局部的能量传导率，而积分形式则关注于流入和流出整体一部分介质的能量。

微分形式

傅立叶定律的微分形式表明了热通量密度正比于热导率乘以负的温度梯度。热通量密度是单位时间内流过单位面积的热量。

$$\overset{\rightarrow}{q} = - K \nabla T$$

这里（使用国际单位制）：

• $\overset{\rightarrow}{q}$ 是热通量密度，单位是 $W \cdot m^{-2}$
• $k$ 是这种材料的热导率，单位是 $W \cdot m^{-1} \cdot K^{-1}$
• $\nabla T$ 是温度梯度，单位是 $K \cdot m^{-1}$

热导 $k$ 通常情况下都被当作是常数，但是实际情况是， $k$ 的值会随温度而变化。然而在很大的温度范围内， $k$ 的变化都可忽略不计。在各向异性介质中，热导率显著地随方向而变化，这时 $k$ 是一个二阶张量。在非均匀介质中， $k$ 与空间位置有关。

在许多情况下，当我们只需考虑一个方向上的热传递（比如 x 方向）时，可用一维傅立叶定律：

$$q_{x} = - k \frac{dT}{dx}$$

积分形式

通过在部分介质表面 $S$ 上对微分式进行积分，我们得到了傅立叶定律的积分形式：

$$P = \frac{\partial Q}{\partial t} = - k \oint_{S} \overset{\rightarrow}{\nabla} T \cdot \overset{\rightarrow}{dA}$$

这里（使用国际单位制）：

• $P=\frac{\partial Q}{\partial t}$ 是热传导功率，即单位时间通过面积 $S$ 的热量，单位是 $W$
• $\overset{\rightarrow}{dA}$ 是面元矢量，单位是 $m^{2}$

当我们所研究的介质是一段两端温度恒定、均匀的一维介质时，积分得到的热传导功率为:

$$P = \frac{\Delta Q}{\Delta t} = -kA\frac{\Delta T}{\Delta x}$$

这里

• $A$ 是介质的截面积
• $\Delta T$ 是两端温差
• $\Delta x$ 是两端距离

这一定律是热传导方程式的基础。

热导

类比于电导，我们可以定义热导 $U$ (单位是 $W/K$ )：

$$U = \frac{k A}{\Delta x} \hspace{50cm}$$

这样傅里叶定律可以写为：

$$P = \frac{\Delta Q}{\Delta t} = U (-\Delta T) \hspace{50cm}$$

热导的倒数是热阻：

$$R = \frac{1}{U} = \frac{\Delta x}{k A} = \frac{- \Delta T}{P} \hspace{50cm}$$

对于由多层不同热阻组成的介质，其总热阻为各层热阻之和，因为通过每层的热传递功率都是相同的。因而总热导与各层热导满足:

$$\frac{1}{U} = \frac{1}{U_{1}} + \frac{1}{U_{2}} +\frac{1}{U_{3}} + \cdot \cdot \cdot \hspace{50cm}$$

所以对于多层介质有：

$$P = \frac{\Delta Q}{\Delta t} = \frac{A(-QT)}{\frac{\Delta_{x_{1}}}{k_{1}} + \frac{\Delta_{x_{2}}}{k_{2}} + \frac{\Delta_{x_{3}}}{k_{3}} + \cdot \cdot \cdot} \hspace{50cm}$$

对于隔着夹层的两种流体之间的热传递，有时必须要考虑到附着与夹层上的流体薄膜的热阻，由于其性质与湍流和粘滞等复杂情况有关，这一流体薄膜非常难于界定。但是当我们考虑薄高热导夹层时，这一影响因素还是很重要的。

热对流

对流传热，又称热对流，是传热的三种方式之一，是指由于流体的宏观运动而引起的流体各部分之间发生相对位移（对流），冷热流体相互掺混所引起的热量传递过程。

对流传热可分为强迫对流和自然对流。强迫对流，是由于外界作用推动下产生的流体循环流动。自然对流是由于温度不同密度梯度变化，重力作用引起低温高密度流体自上而下流动，高温低密度流体自下而上流动。

热辐射

热辐射（英语：Thermal radiation）是物体用电磁辐射把热能向外散发的热传方式，是热的三种主要传递方式之一，以热辐射传递热时不需要介质。任何物体温度只要高于 0 开尔文就会释放热辐射。

热辐射速率

辐射物的功率 $P_{rad} = \epsilon \sigma A T^{4}$ 。
其中：

• $T$ 为绝对温度（开尔文）
• $A$ 为物体表面积（平方米）；
• $\sigma = 5.6704 \times 10^{-8} W \cdot m^{-2} \cdot K^{-4}$ 为斯特藩·波尔兹曼常数。
• $\epsilon$ 为物体表面放射率（介于 0 ~ 1），黑体辐射为 1 。

热导率（热传导率）

热导率（英语：Thermal conductivity）其符号为 $k$ 、 $\lambda$ 或 $\kappa$ ，是指材料传导热能的能力，或称热传导率。单位是瓦·米^-1·开尔文^-1 ( $\dfrac{W}{mK}$ )。

定义

热导率为在单位时间内，每单位截面积所流过的热量除以单位距离温度变化量的负值。由傅里叶定律：

$$q = - k \nabla T$$

其中 $q$ 为热通量密度，矢量； $k$ 是热导率； $\nabla T$ 是温度梯度，矢量。

若给定两物质，其坐标分别为 $x=0$ 与 $x=L>0$，其温度分别为 $T_{1}$ 与 $T_{2}$ ，且 $T_{2}>T_{1}$ 。
则可将等式转换为：

$$q = - k \cdot \frac{T_{2} - T_{1}}{L}$$

根据热力学第二定律，热量由高温物体向低温物体传递，所以在此处 $q<0$ ，则可推知 $k>0$ 。

影响热导率的因素

温度

热导率会随着温度升高，并且可以在一特定温度范围内维持在最大值，然而温度一旦超过此一范围，热导率会快速衰减至最小值，此时温度则接近该物质熔点。

晶粒大小

热导率会随着晶粒增大而增加。

晶形

除了立方晶系（cubic system）的物质，多数物质之热导率具有非均向性（anisotropy）。

化学组成（杂质含量，纯度）

热导率受杂质影响甚巨。

典型物质的热导率

热扩散率

在热传分析中，热扩散率（符号：$\alpha$ ，但注意 $\kappa$ 、 $D$ 和 $k$ 都很常用）是热导率和容积热容之比，单位是（ $m^2/s$ ）：

$$\alpha = \frac{k}{\rho c_p}$$

其中：

• $k$ ： 热导率，单位是（ $W \cdot m^{-1} \cdot K^{-1}$ ）
• $\rho c_p$ ： 容积热容，单位是（ $J \cdot m^{-3} \cdot K^{-1}$ ）
• $\rho$ ： 密度，单位是（ $kg \cdot m^{-3}$）
• $c_p$ ： 比热容，单位是（ $J \cdot kg^{-1} \cdot K^{-1}$）

影响热扩散率的因素

热导率

物质的热导率对热扩散率有很大的影响，具有高热导率的物质往往会有比较大的热扩散率。

材料的结构和组成

对于非单一物质的材料来说，其结构和组成也会影响热扩散率。晶体结构的不同会导致热导率性能的差异。晶体中的原子或离子之间相对固定的排列结构使其热传能力增强。此外，材料中的异质性也会对热扩散率产生影响。异质性会导致材料引入界面、缺陷和杂质，从而对热传导过程造成干扰。

温度

温度也会影响热扩散率，通常情况下温度升高会导致热扩散率的增加。因为温度随着温度的升高，原子的震动变得更加激烈，这必将会导致能量传递的更快。

压力

压力同温度对热扩散率的影响相似，高压下，分子之间的间距减小，振动频率增加，热扩散率随之也会相应增加。

典型材料与物质的热扩散率

问题讨论

温度对热扩散的影响

温度对热扩散的影响主要体现在其对材料热导率、热扩散率以及分子运动等的影响上。

对于热导率的影响

对于各类绝热材料来讲，温度对其热导率有着直接的影响。随着温度的升高，材料的分子热运动增强，材料空隙中空气的导热和孔壁间的辐射作用也会有所增加，导致热导率上升。此时绝热材料的绝热性能会逐渐下降。这种影响在 0 ~ 50℃ 范围内并不显著，但对于高温和负温环境下，影响较为明显。

对于热扩散率的影响

温度越高，热扩散率会越大，扩散速度越快。是因为温度的升高加速了分子热运动，使得分子间的相互作用更加频繁剧烈，此时必然会加速物质的扩散过程。相反，温度降低时，分子热运动将减慢，扩散速度也会变小。

对于分子运动的影响

上述两种影响种也提到，温度的升高会加速分子热运动速度，其平均动能也会增加。而分子热运动会导致物质的扩散，在固体中，分子之间的作用力很强，只有在极高温下才能克服这种作用力发生扩散；在液体中，分子之间的作用力较弱，温度升高物质的扩散速度增大；在气体中，分子之间的相互作用很弱，高温会使分子热运动急剧增加，扩散速度随之增大。